EM Algorithm
Published:
老实说,EM算法这玩意曾经一直是我心里一个坑,学了至少三遍 (周志华西瓜书第一遍,李航《统计学习方法》第二遍,过了一年又回顾了一遍) 才有了比较清楚的思路。跟着各种教程一行行看很容易陷入推导长长的公式的泥沼,到头来知道中间有用Jensen不等式放缩,知道要优化一个下界函数,但具体谈起细节来又不是那么清楚。这里我试图把我学习三次之后的理解分享一下,提供我自己理解EM算法的视角。
当然,看完这篇还是不懂EM也是正常的,一来我水平有限,二来学习知识本来就是螺旋上升的过程。刚开始懵懵懂懂地记住一些东西,以后随着知识和项目的积累,回过头来再看这部分内容,也许哪一天就醍醐灌顶了。
EM算法概览
MLE
在正式接触EM算法之前,我们先回顾一下概率统计里面经典的参数估计方法——最大化似然估计 (Maximum Likelihood Estimation)。这里所谓似然,就是指概率。实际上意思是说,我们现在有一个分布,但是参数未知,要估计这些参数,手头有的数据是从这个分布中采样得到的一些样本,那么通过最大化这些样本出现的概率来确定参数值。
举个例子,如果全校男生身高是服从高斯分布的,但我们不知道高斯分布的两个参数:均值 \(\mu\) 和方差 \(\sigma\),所以怎么办呢?既然已经有了概率分布的公式 (尽管有两个参数未知),那么就按照高中数学中变量和参数的视角 (函数中将 \(x\) 看作自变量,其他未知数,比如 \(a\) 都看作已知的参数),将这两个参数看成已知,求出这些男生的身高刚好是这些值的概率 (如果男生身高为 \(x\) 的概率为 \(p(x\vert\mu, \sigma)\)):
\[p(X) = p(x_1|\mu, \sigma) p(x_2|\mu, \sigma) ... p(x_n|\mu, \sigma)\]那么好,这个 \(p(X)\),即样本点取这些值的概率,就是关于参数 \(\mu\) 和 \(\sigma\) 的函数,直接最大化这个概率就可以求出参数的估计值了,即:
\[\theta = \mathop{argmax}_\theta \quad p(X)\]实际求解的时候还是取了 log,使得连乘变成求和,这样求导就比较方便。 所以说参数其实是选取的一组使得样本出现概率最大的值。
从 MLE 到 EM
那么直接用 MLE 有啥问题吗?EM 算法是解决什么问题的呢? 问题在于“隐变量”这个小可爱的出现,让似然的计算式里多出了隐变量的部分,无法直接对似然求最大。隐变量不属于模型参数,是无法直接观测到的,但又和参数一起对采样结果有直接的影响。
还是举例来说明,经典的三硬币问题: 有三枚硬币 A,B,C (正面率不一定是 1/2),先投掷 A,如果是正面就投掷 B,如果是反面就投掷 C,若我们只能观测到最后的投掷结果 (B 或者 C 的结果),如何估算三颗硬币的正面率? 这里每次 A 的结果不能从观测变量中直接得到,因此A是一个隐变量。似然的计算式中就会出现 \(p(A是正面)\)、\(p(B是正面|A是正面)\) 等部分,无法全部用模型参数来表示了。
EM 的总体思路
针对隐变量的问题,EM 算法的总体思路是这样的:
- 初始化:给模型参数一个初始值
- 用已有的参数估计隐变量的值 (E步)
- 把估计的隐变量作为已知,最大化似然,更新模型参数 (M步)
- 不断重复第2、3步,直至收敛 (比如参数变化很小)
EM 算法的推导
上面只是介绍了总体的思路,还是有很多问题,比如,为什么这么算是有效的?迭代下来似然一定会递增吗?具体如何最大化似然? 接下来就对EM算法进行一下推导和证明。
Auxiliary Function Q
规定概率模型参数为 \(\theta\),共有 \(m\) 个样本:\(x^{(1)}, x^{(2)}, ..., x^{(i)}, ..., x^{(m)}\),隐变量为 \(z\),似然为 \(L(\theta)\)。 那么要最大化的似然就是
\[L(\theta) = \sum_{i=1}^m log P(x^{(i)}|\theta)\]考虑隐变量 \(z\) 的影响,那么 \(P(x^{(i)}\vert\theta) = \sum \limits_{z^{(i)}}P(x^{(i)}, z^{(i)}\vert\theta)\),所以
\[L(\theta) = \sum_{i=1}^m log[\sum_{z^{(i)}}P(x^{(i)}, z^{(i)}|\theta)]\]下面是关键的一步,规定 \(\hat\theta\) 为当前的参数值,可能是初始值也可能是迭代了几轮之后的参数值,总之是一组确定的值,那么
\[log P(x^{(i)}|\theta) = log\sum_{z^{(i)}}P(x^{(i)}, z^{(i)}|\theta) = log\sum_{z^{(i)}}[P(z^{(i)}|x^{(i)}, \hat\theta)\frac{P(x^{(i)}, z^{(i)}|\theta)}{P(z^{(i)}|x^{(i)}, \hat\theta)}]\]看到这大概要奇怪了,为啥要做先乘后除 \(P(z^{(i)}|x^{(i)}, \hat\theta)\) 这部分的操作呢?这就需要介绍著名的 Jensen 不等式了。 Jensen不等式可以通过凸函数的图像很直观地得出,这里就不讨论一般形式了,直接给出和 EM 算法有关的在 log 函数下的形式:
\[\sum_i^n\alpha_ilogx_i \leq log\sum_i^n\alpha_ix_i\]其中 \(\alpha\) 满足 \(\sum \limits_{i=1}\limits^n\alpha_i = 1\),当且仅当 \(x_1 = x_2 = \ldots = x_n\) 时取等号。 这个不等式有个好处:右边是和的对数,经过放缩之后变成了对数的和。而实际上,\(\sum \limits_{z^{(i)}}P(z^{(i)}|x^{(i)}, \hat\theta) = 1\),隐变量取到各个值的概率之和是 1,刚好满足这个条件,这样一来应用 Jensen 不等式,\(logP(x^{(i)}|\theta)\) 就转化成对数之和的形式,对 \(\theta\) 的优化就更加容易:
\[log\sum_{z^{(i)}}[P(z^{(i)}|x^{(i)}, \hat\theta)\frac{P(x^{(i)}, z^{(i)}|\theta)}{P(z^{(i)}|x^{(i)}, \hat\theta)}] \geq \sum_{z^(i)}P(z^{(i)}|x^{(i)}, \hat\theta)log\frac{P(x^{(i)}, z^{(i)}|\theta)}{P(z^{(i)}|x^{(i)}, \hat\theta)}\]所以
\[L(\theta) \geq \sum_{i=1}^m\sum_{z^{(i)}}P(z^{(i)}|x^{(i)}, \hat\theta)log\frac{P(x^{(i)}, z^{(i)}|\theta)}{P(z^{(i)}|x^{(i)}, \hat\theta)}\]于是我们成功地为原来难以直接优化的似然函数 \(L(\theta)\) 找到了一个形式为对数之和的,更好优化的下界 (虽然推导过程看起来像强行凑 Jensen 不等式,但数学上很多推导就是这么巧…),不妨称之为 \(B(\theta)\)。 注意到 \(\hat\theta\) 是确定的值,所以上式中只有 \(P(x^{(i)}, z^{(i)}|\theta)\) 是不确定的部分,提出这部分就能得到我们的辅助函数 (Auxiliary Function) Q:
\[Q(\theta) = \sum_{i=1}^m\sum_{z^{(i)}}P(z^{(i)}|x^{(i)}, \hat\theta)logP(x^{(i)}, z^{(i)}|\theta)\]没错,真正用 MLE 的思路来求参数就是对这个 Auxiliary Function \(Q(\theta)\),而不是对原始的似然函数 \(L(\theta)\) 求极大。
取等号的条件
看到这里,好像有哪里不太对:通过 Jensen 不等式能够放缩到一个对数之和的$B$函数的形式,但是仅仅满足 \(L(\theta) \geq B(\theta)\) 这个条件,对 \(Q\) 求极大(也就是对 \(B\) 求极大)得到的 \(\theta\) 并不能保证 \(L\) 也增大呀。事实上,刚刚不等式放缩的过程中的确有一项内容被忽略了:取等号的条件。 将 \(x_1 = x_2 = \ldots = x_n\) 的条件应用到这里,就是对于各个 \(z^{(i)}\),\(\frac{P(x^{(i)}, z^{(i)} | \theta)}{P(z^{(i)} | x^{(i)}, \hat\theta)}\) 都相等,不妨令
\[\frac{P(x^{(i)}, z^{(i)}\vert\theta)}{P(z^{(i)}\vert x^{(i)}, \hat\theta)} = c \text{(constant)}\] \[P(x^{(i)}, z^{(i)}\vert\theta) = c\cdot P(z^{(i)}\vert x^{(i)}, \hat\theta)\]等式两边同时对 \(z^{(i)}\) 求和:
\[\sum_{z^{(i)}}^{}P(x^{(i)}, z^{(i)}\vert\theta) = c \sum_{z^{(i)}}P(z^{(i)}\vert x^{(i)}, \hat\theta)\] \[P(x^{(i)}|\theta) = c\]求得常数 c 之后再把 c 回带到上面的等式中:
\[P(x^{(i)}\vert\theta) = \frac{P(x^{(i)}, z^{(i)}\vert\theta)}{P(z^{(i)}\vert x^{(i)}, \hat\theta)}\] \[P(z^{(i)}\vert x^{(i)}, \hat\theta) = \frac{P(x^{(i)}, z^{(i)}\vert\theta)}{P(x^{(i)}\vert\theta)} = P(z^{(i)}\vert x^{(i)}, \theta)\]于是我们得到取等号的条件实际上就是:
\[\theta = \hat\theta\]当参数值取当前参数的时候,Jensen不等式取等号!
图形角度看EM算法
换个视角来看,\(L(\theta)\) 和 \(B(\theta)\) 都是关于 \(\theta\) 的函数,它们满足(1) \(L(\theta) \geq B(\theta)\) (2) 只有一个点满足两者相等,即 \(\hat\theta\) 那么画个图,就能很轻松地看出优化过程中 \(B(\theta)\) 的变化了:
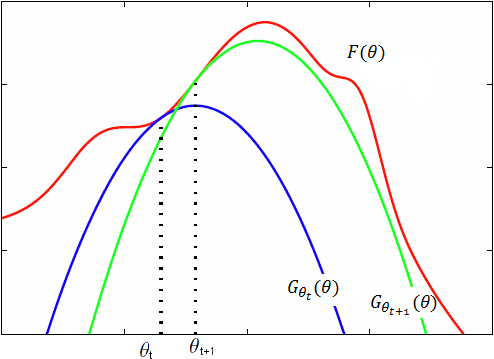
图片是我从网上随便找的,符号和前面略有不同,图中红色的 \(F\) 对应前面的目标似然函数 \(L\),蓝色和绿色的两条$G$对应前面的下界函数 \(B\),注意到 \(B\) 也受 \(\hat\theta\) 的影响,每一轮的 \(B\) 函数是不一样的,蓝色的线对应第 t 轮,绿色的线对应第 t+1 轮。 这张图很好地反映了 \(B\) 的变化:每一轮迭代之前,\(L\) 和 \(B\) 是相等的,经过一次迭代,\(\theta\) 跑到了 \(B\) 取得极大的位置,而 \(L(\theta) \geq B(\theta)\),所以 \(L(\theta)\) 也变大了。于是到下一轮,新的 \(B\) 函数在新的 \(\theta\) 处又和 \(L\) 相等,进入了和上次迭代之前相同的状态。如此不断迭代下去,\(L(\theta)\) 就不断变大,朝着我们最初最大化似然的目标不断前进。
数学证明
什么,你说这样不够严谨?好,那从数学角度证明一遍 \(L(\theta)\) 递增呗。 令 \(\theta^{t+1}\) 和 \(\theta^t\) 分别表示第 t+1 轮和第 t 轮的参数值,那么需要证明的就是 \(L(\theta^{t+1}) \geq L(\theta^t)\)。 由于 \(\theta^{t+1}\) 定义就是对 \(Q(\theta, \theta^t)\) 求极大得到的,所以 \(Q(\theta^{t+1}, \theta^t) \geq Q(\theta^t, \theta^t)\) 天然成立,不妨看看 \(L(\theta)\) 和 \(Q(\theta, \theta^t)\) 相比差了啥:
\[L(\theta) = \sum_{i=1}^m log P(x^{(i)}\vert\theta)\] \[Q(\theta, \theta^t) = \sum_{i=1}^m\sum_{z^{(i)}}P(z^{(i)}\vert x^{(i)}, \theta^t)logP(x^{(i)}, z^{(i)}\vert\theta)\]把 \(L(\theta)\) 也加上对 \(z^{(i)}\) 求和的部分,和 \(Q(\theta, \theta^t)\) 对应起来:
\[L(\theta) = \sum_{i=1}^m\sum_{z^{(i)}}P(z^{(i)}\vert x^{(i)}, \theta^t)log P(x^{(i)}\vert\theta)\]然后两式相减,得到:
\[Q(\theta, \theta^t) - L(\theta) = \sum_{i=1}^m\sum_{z^{(i)}}P(z^{(i)}|x^{(i)}, \theta^t) log\frac{P(x^{(i)}, z^{(i)}|\theta)}{P(x^{(i)}|\theta)} = \sum_{i=1}^m\sum_{z^{(i)}}P(z^{(i)}|x^{(i)}, \theta^t) logP(z^{(i)}|x^{(i)}, \theta)\]令这个函数为 \(H(\theta, \theta^t)\) (如果了解信息熵会发现真的很符合信息熵的定义啊,叫 H 没毛病),所以
\[L(\theta) = Q(\theta, \theta^t) - H(\theta, \theta^t)\] \[L(\theta^{t+1}) - L(\theta^t) = [Q(\theta^{t+1}, \theta^t) - Q(\theta^t, \theta^t)] - [H(\theta^{t+1}, \theta^t) - H(\theta^t, \theta^t)]\]第一项已经是非负了,so 只要保证第二项非正即可。于是:
\[\begin{align} H(\theta^{t+1}, \theta^t) - H(\theta^t, \theta^t) &= \sum_{i=1}^m\sum_{z^{(i)}}P(z^{(i)}|x^{(i)}, \theta^t)log\frac{P(z^{(i)}|x^{(i)}, \theta^{t+1})}{P(z^{(i)}|x^{(i)}, \theta^t)} \\ &\leq \sum_{i=1}^mlog\sum_{z^{(i)}}P(z^{(i)}|x^{(i)}, \theta^t)\frac{P(z^{(i)}|x^{(i)}, \theta^{t+1})}{P(z^{(i)}|x^{(i)}, \theta^t)} \\ &=\sum_{i=1}log\sum_{z^{(i)}}P(z^{(i)}|x^{(i)}, \theta^{t+1}) \\ &=0 \\ \end{align}\]很好,这里又用了一次Jensen不等式,和前面一样,也是因为隐变量取到各个值概率之和为1。于是第二项顺利证出非正,\(L(\theta)\) 似然函数的递增性证明完成。
EM算法的应用
恭喜,经过一大波公式,我们已经成功地推导并证明了EM算法。当然,上面推导的过程中,也可以先不给出 \(P(z^{(i)}|x^{(i)}, \hat\theta)\) 这个式子,而是按照 Jensen 不等式的条件,假设有个跟 \(z^{(i)}\) 有关的表达式,比如叫 \(F(z^{(i)})\),加起来为1,这样直接用 Jensen 不等式放缩,最后求取等号的条件会发现,\(F(z^{(i)}) = P(z^{(i)}|x^{(i)}, \hat\theta)\),同样得出这个因子就是隐变量在样本和当前参数下的分布,看到有些教程就是按这个思路来写的。 这样一来,上面写的EM算法的总体思路就很好理解了,核心就是进行这样的迭代: (1) 用样本和当前参数估计每个样本隐变量 \(z^{(i)}\) 的分布 (2) 以隐变量的分布为已知,优化$Q$函数,求出此时使 \(Q\) 最大的参数 \(\theta\),作为下一轮迭代的初始参数
