老实说,EM算法这玩意曾经一直是我心里一个坑,学了至少三遍 (周志华西瓜书第一遍,李航《统计学习方法》第二遍,过了一年又回顾了一遍) 才有了比较清楚的思路。跟着各种教程一行行看很容易陷入推导长长的公式的泥沼,到头来知道中间有用Jensen不等式放缩,知道要优化一个下界函数,但具体谈起细节来又不是那么清楚。这里我试图把我学习三次之后的理解分享一下,提供我自己理解EM算法的视角。
当然,看完这篇还是不懂EM也是正常的,一来我水平有限,二来学习知识本来就是螺旋上升的过程。刚开始懵懵懂懂地记住一些东西,以后随着知识和项目的积累,回过头来再看这部分内容,也许哪一天就醍醐灌顶了。
EM算法概览
MLE
在正式接触EM算法之前,我们先回顾一下概率统计里面经典的参数估计方法——最大化似然估计 (Maximum Likelihood Estimation)。这里所谓似然,就是指概率。实际上意思是说,我们现在有一个分布,但是参数未知,要估计这些参数,手头有的数据是从这个分布中采样得到的一些样本,那么通过最大化这些样本出现的概率来确定参数值。
举个例子,如果全校男生身高是服从高斯分布的,但我们不知道高斯分布的两个参数:均值$\mu$和方差$\sigma$,所以怎么办呢?既然已经有了概率分布的公式 (尽管有两个参数未知),那么就按照高中数学中变量和参数的视角 (函数中将$x$看作自变量,其他未知数,比如$a$都看作已知的参数),将这两个参数看成已知,求出这些男生的身高刚好是这些值的概率 (如果男生身高为$x$的概率为$p(x|\mu, \sigma)$):
$$p(X) = p(x_1|\mu, \sigma) p(x_2|\mu, \sigma) … p(x_n|\mu, \sigma)$$
那么好,这个$p(X)$,即样本点取这些值的概率,就是关于参数$\mu$和$\sigma$的函数,直接最大化这个概率就可以求出参数的估计值了,即:
$$\theta = \mathop{argmax}_\theta p(X)$$
实际求解的时候还是取了log,使得连乘变成求和,这样求导就比较方便。
所以说参数其实是选取的一组使得样本出现概率最大的值。
从MLE到EM
那么直接用MLE有啥问题吗?EM算法是解决什么问题的呢?
问题在于“隐变量”这个小可爱的出现,让似然的计算式里多出了隐变量的部分,无法直接对似然求最大。隐变量不属于模型参数,是无法直接观测到的,但又和参数一起对采样结果有直接的影响。
还是举例来说明,经典的三硬币问题:
有三枚硬币A,B,C (正面率不一定是1/2),先投掷A,如果是正面就投掷B,如果是反面就投掷C,若我们只能观测到最后的投掷结果 (B或者C的结果),如何估算三颗硬币的正面率?
这里每次A的结果不能从观测变量中直接得到,因此A是一个隐变量。似然的计算式中就会出现$p(A是正面)$、$p(B是正面|A是正面)$等部分,无法全部用模型参数来表示了。
EM的总体思路
针对隐变量的问题,EM算法的总体思路是这样的:
- 初始化:给模型参数一个初始值
- 用已有的参数估计隐变量的值 (E步)
- 把估计的隐变量作为已知,最大化似然,更新模型参数 (M步)
- 不断重复第2、3步,直至收敛 (比如参数变化很小)
EM算法的推导
上面只是介绍了总体的思路,还是有很多问题,比如,为什么这么算是有效的?迭代下来似然一定会递增吗?具体如何最大化似然?
接下来就对EM算法进行一下推导和证明。
Auxiliary Function Q
规定概率模型参数为$\theta$,共有$m$个样本:$x^{(1)}, x^{(2)},…, x^{(i)},…,x^{(m)}$,隐变量为$z$,似然为$L(\theta)$。
那么要最大化的似然就是
$$L(\theta) = \sum_{i=1}^m log P(x^{(i)}|\theta)$$
考虑隐变量$z$的影响,那么$P(x^{(i)}|\theta) = \sum \limits_{z^{(i)}}P(x^{(i)}, z^{(i)}|\theta)$,所以
$$L(\theta) = \sum_{i=1}^m log[\sum_{z^{(i)}}P(x^{(i)}, z^{(i)}|\theta)]$$
下面是关键的一步,规定$\hat\theta$为当前的参数值,可能是初始值也可能是迭代了几轮之后的参数值,总之是一组确定的值,那么
$$log P(x^{(i)}|\theta) = log\sum_{z^{(i)}}P(x^{(i)}, z^{(i)}|\theta) = log\sum_{z^{(i)}}[P(z^{(i)}|x^{(i)}, \hat\theta)\frac{P(x^{(i)}, z^{(i)}|\theta)}{P(z^{(i)}|x^{(i)}, \hat\theta)}]$$
看到这大概要奇怪了,为啥要做先乘后除$P(z^{(i)}|x^{(i)}, \hat\theta)$这部分的操作呢?这就需要介绍著名的Jensen不等式了。
Jensen不等式可以通过凸函数的图像很直观地得出,这里就不讨论一般形式了,直接给出和EM算法有关的在log函数下的形式:
$$\sum_i^n\alpha_ilogx_i \leq log\sum_i^n\alpha_ix_i$$
其中$\alpha$满足$\sum \limits_{i=1}\limits^n\alpha_i = 1$,当且仅当$x_1 = x_2 = \ldots = x_n$时取等号。
这个不等式有个好处:右边是和的对数,经过放缩之后变成了对数的和。而实际上,$\sum \limits_{z^{(i)}}P(z^{(i)}|x^{(i)}, \hat\theta) = 1$,隐变量取到各个值的概率之和是1,刚好满足这个条件,这样一来应用Jensen不等式,$logP(x^{(i)}|\theta)$就转化成对数之和的形式,对$\theta$的优化就更加容易:
$$log\sum_{z^{(i)}}[P(z^{(i)}|x^{(i)}, \hat\theta)\frac{P(x^{(i)}, z^{(i)}|\theta)}{P(z^{(i)}|x^{(i)}, \hat\theta)}] \geq \sum_{z^(i)}P(z^{(i)}|x^{(i)}, \hat\theta)log\frac{P(x^{(i)}, z^{(i)}|\theta)}{P(z^{(i)}|x^{(i)}, \hat\theta)}$$
所以
$$L(\theta) \geq \sum_{i=1}^m\sum_{z^{(i)}}P(z^{(i)}|x^{(i)}, \hat\theta)log\frac{P(x^{(i)}, z^{(i)}|\theta)}{P(z^{(i)}|x^{(i)}, \hat\theta)}$$
于是我们成功地为原来难以直接优化的似然函数$L(\theta)$找到了一个形式为对数之和的,更好优化的下界 (虽然推导过程看起来像强行凑Jensen不等式,但数学上很多推导就是这么巧…),不妨称之为$B(\theta)$。
注意到$\hat\theta$是确定的值,所以上式中只有$P(x^{(i)}, z^{(i)}|\theta)$是不确定的部分,提出这部分就能得到我们的辅助函数 (Auxiliary Function) Q:
$$Q(\theta) = \sum_{i=1}^m\sum_{z^{(i)}}P(z^{(i)}|x^{(i)}, \hat\theta)logP(x^{(i)}, z^{(i)}|\theta)$$
没错,真正用 MLE 的思路来求参数就是对这个 Auxiliary Function $Q(\theta)$,而不是对原始的似然函数$L(\theta)$求极大。
取等号的条件
看到这里,好像有哪里不太对:通过Jensen不等式能够放缩到一个对数之和的$B$函数的形式,但是仅仅满足$L(\theta) \geq B(\theta)$这个条件,对$Q$求极大(也就是对$B$求极大)得到的$\theta$并不能保证$L$也增大呀。事实上,刚刚不等式放缩的过程中的确有一项内容被忽略了:取等号的条件。
将$x_1 = x_2 = \ldots = x_n$的条件应用到这里,就是对于各个$z^{(i)}$,$\frac{P(x^{(i)}, z^{(i)} | \theta)}{P(z^{(i)} | x^{(i)}, \hat\theta)}$都相等,不妨令
$$\frac{P(x^{(i)}, z^{(i)}|\theta)}{P(z^{(i)}|x^{(i)}, \hat\theta)} = c (constant)$$
$$P(x^{(i)}, z^{(i)}|\theta) = c\cdot P(z^{(i)}|x^{(i)}, \hat\theta)$$
等式两边同时对$z^{(i)}$求和:
$$\sum_{z^{(i)}}P(x^{(i)}, z^{(i)}|\theta) = c \sum_{z^{(i)}}P(z^{(i)}|x^{(i)}, \hat\theta)$$
$$P(x^{(i)}|\theta) = c$$
求得常数c之后再把c回带到上面的等式中:
$$P(x^{(i)}|\theta) = \frac{P(x^{(i)}, z^{(i)}|\theta)}{P(z^{(i)}|x^{(i)}, \hat\theta)}$$
$$P(z^{(i)}|x^{(i)}, \hat\theta) = \frac{P(x^{(i)}, z^{(i)}|\theta)}{P(x^{(i)}|\theta)} = P(z^{(i)}|x^{(i)}, \theta)$$
于是我们得到取等号的条件实际上就是:
$$\theta = \hat\theta$$
当参数值取当前参数的时候,Jensen不等式取等号!
图形角度看EM算法
换个视角来看,$L(\theta)$和$B(\theta)$都是关于$\theta$的函数,它们满足(1) $L(\theta) \geq B(\theta)$ (2) 只有一个点满足两者相等,即$\hat\theta$
那么画个图,就能很轻松地看出优化过程中$B(\theta)$的变化了: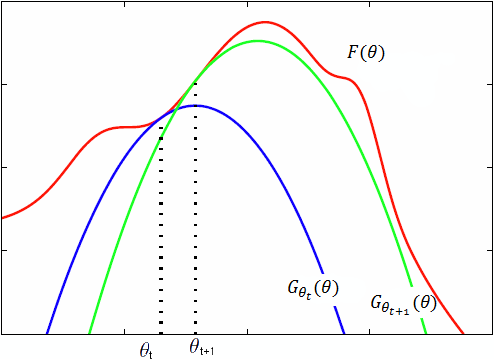
图片是我从网上随便找的,符号和前面略有不同,图中红色的$F$对应前面的目标似然函数$L$,蓝色和绿色的两条$G$对应前面的下界函数$B$,注意到$B$也受$\hat\theta$的影响,每一轮的$B$函数是不一样的,蓝色的线对应第t轮,绿色的线对应第t+1轮。
这张图很好地反映了$B$的变化:每一轮迭代之前,$L$和$B$是相等的,经过一次迭代,$\theta$跑到了$B$取得极大的位置,而$L(\theta) \geq B(\theta)$,所以$L(\theta)$也变大了。于是到下一轮,新的$B$函数在新的$\theta$处又和$L$相等,进入了和上次迭代之前相同的状态。如此不断迭代下去,$L(\theta)$就不断变大,朝着我们最初最大化似然的目标不断前进。
数学证明
什么,你说这样不够严谨?好,那从数学角度证明一遍$L(\theta)$递增呗。
令$\theta^{t+1}$和$\theta^t$分别表示第t+1轮和第t轮的参数值,那么需要证明的就是$L(\theta^{t+1}) \geq L(\theta^t)$。
由于$\theta^{t+1}$定义就是对$Q(\theta, \theta^t)$求极大得到的,所以$Q(\theta^{t+1}, \theta^t) \geq Q(\theta^t, \theta^t)$天然成立,不妨看看$L(\theta)$和$Q(\theta, \theta^t)$相比差了啥:
$$L(\theta) = \sum_{i=1}^m log P(x^{(i)}|\theta)$$
$$Q(\theta, \theta^t) = \sum_{i=1}^m\sum_{z^{(i)}}P(z^{(i)}|x^{(i)}, \theta^t)logP(x^{(i)}, z^{(i)}|\theta)$$
把$L(\theta)$也加上对$z^{(i)}$求和的部分,和$Q(\theta, \theta^t)$对应起来:
$$L(\theta) = \sum_{i=1}^m\sum_{z^{(i)}}P(z^{(i)}|x^{(i)}, \theta^t)log P(x^{(i)}|\theta)$$
然后两式相减,得到:
$$Q(\theta, \theta^t) - L(\theta) = \sum_{i=1}^m\sum_{z^{(i)}}P(z^{(i)}|x^{(i)}, \theta^t) log\frac{P(x^{(i)}, z^{(i)}|\theta)}{P(x^{(i)}|\theta)} = \sum_{i=1}^m\sum_{z^{(i)}}P(z^{(i)}|x^{(i)}, \theta^t) logP(z^{(i)}|x^{(i)}, \theta)$$
令这个函数为$H(\theta, \theta^t)$(如果了解信息熵会发现真的很符合信息熵的定义啊,叫H没毛病),所以
$$L(\theta) = Q(\theta, \theta^t) - H(\theta, \theta^t)$$
$$L(\theta^{t+1}) - L(\theta^t) = [Q(\theta^{t+1}, \theta^t) - Q(\theta^t, \theta^t)] - [H(\theta^{t+1}, \theta^t) - H(\theta^t, \theta^t)]$$
第一项已经是非负了,so只要保证第二项非正即可。于是:
\begin{equation}\begin{split}
H(\theta^{t+1}, \theta^t) - H(\theta^t, \theta^t) &= \sum_{i=1}^m\sum_{z^{(i)}}P(z^{(i)}|x^{(i)}, \theta^t)log\frac{P(z^{(i)}|x^{(i)}, \theta^{t+1})}{P(z^{(i)}|x^{(i)}, \theta^t)}\\
&\leq \sum_{i=1}^mlog\sum_{z^{(i)}}P(z^{(i)}|x^{(i)}, \theta^t)\frac{P(z^{(i)}|x^{(i)}, \theta^{t+1})}{P(z^{(i)}|x^{(i)}, \theta^t)}\\
&=\sum_{i=1}log\sum_{z^{(i)}}P(z^{(i)}|x^{(i)}, \theta^{t+1})\\
&=0\\
\end{split}\end{equation}
很好,这里又用了一次Jensen不等式,和前面一样,也是因为隐变量取到各个值概率之和为1。于是第二项顺利证出非正,$L(\theta)$似然函数的递增性证明完成。
EM算法的应用
恭喜,经过一大波公式,我们已经成功地推导并证明了EM算法。当然,上面推导的过程中,也可以先不给出$P(z^{(i)}|x^{(i)}, \hat\theta)$这个式子,而是按照Jensen不等式的条件,假设有个跟$z^{(i)}$有关的表达式,比如叫$F(z^{(i)})$,加起来为1,这样直接用Jensen不等式放缩,最后求取等号的条件会发现,$F(z^{(i)}) = P(z^{(i)}|x^{(i)}, \hat\theta)$,同样得出这个因子就是隐变量在样本和当前参数下的分布,看到有些教程就是按这个思路来写的。
这样一来,上面写的EM算法的总体思路就很好理解了,核心就是进行这样的迭代:
(1) 用样本和当前参数估计每个样本隐变量$z^{(i)}$的分布
(2) 以隐变量的分布为已知,优化$Q$函数,求出此时使$Q$最大的参数$\theta$,作为下一轮迭代的初始参数
在我所接触的语音这一块,EM算法有两个经典的应用:(1) GMM模型的参数求解 (2) HMM模型的参数求解
在此先挖个坑,在接下来的两篇中将会简要地推导一下EM算法在GMM和HMM中的求解过程。。。